Basic Data Structures
My Take on UCSD's Basic Data Structures course (CSE 12)
Project maintained by nate-browne Hosted on GitHub Pages — Theme by mattgraham
Rebalancing Binary Search Trees
Chapters 4 and 12 of Data Structures and Algorithm Analysis in C++
(Partially) Implementing a Binary Search Tree
Last lecture, we talked about the concepts underlying a binary search tree. This lecture, we’ll implement some features (and you’ll do the rest in your PA!)
Firstly, let’s define our class. Our in-class BST will only hold integers, though your PA uses templates.
We’ll define our methods as virtual, so that we can do subtyping in the future if we choose (hint hint);
class BST {
struct BSTNode {
int element;
BSTNode *left, *right;
int height;
BSTNode(int el, BSTNode *lt = nullptr, BSTNode *rt = nullptr) : element(el), left(lt), right(rt) {
this->height = 0;
}
~BSTNode(void) { }
};
BSTNode *root;
virtual int height(BSTNode *t) const;
virtual void balance(BSTNode *& t);
virtual void insert(const int x, BSTNode *& t);
virtual BSTNode * find_min_rec(BSTNode *t) const;
virtual BSTNode * find_min_iter(BSTNode *t) const;
virtual bool contains(const int x, BSTNode *t) const;
public:
BST(void);
virtual ~BST(void);
virtual const int find_min(void) const;
virtual bool contains(const int x) const;
virtual void insert(const int x);
// other private and public methods omitted
// that's for you to do in your PA :)
};
Great! Any questions about our class as we’ve defined it so far?
Let’s start by implementing the private methods one by one. We’ll go in order from top to bottom.
int BST::height(BSTNode *t) const {
return (t) ? t->height : -1; // null node has height -1
}
void BST::balance(BSTNode *& t) {
if(!t) return; // base case
t->height = std::max(height(t->left), height(t->right)) + 1;
}
These are two pretty simple helper methods, but we need these to do insert. Speaking of which, how do we approach insert?
void BST::insert(const int x, BSTNode *& t) {
// base case
if(!t) {
t = new BSTNode(x); // why does this work?
} else if(x < t->element) {
insert(x, t->left);
} else if(t->element < x) {
insert(x, t->right);
}
// set height
this->balance(t);
}
void BST::insert(const int x) {
this->insert(x, this->root);
}
Does this insert implementation work?
Next, constructor and destructor:
BST::BST(void) : root(nullptr) { }
BST::~BST(void) {
this->empty(); // empty and 1 arg empty omitted
}
Easy enough, eh? Let’s do the find_min functions next:
// this is given in your PA
const int BST::find_min(void) const {
if(this->root) return this->find_min_rec(this->root)->element;
else throw std::out_of_range("Tree has no elements.");
}
BSTNode * BST::find_min_rec(BSTNode *t) const {
// smallest is found by going left
if(!t->left) return t;
return find_min_rec(t->left);
}
BSTNode * BST::find_min_iter(BSTNode *t) const {
// smallest is found by going left
while(t->left) t = t->left;
return t;
}
As you can see, this function is pretty straight forward both iteratively and recursively.
As a fun fact, the recursive one would (if compiled with optimizations on) get turned into the iterative one by the compiler due to tail call optimization, but that is a subject for a programming languages course or a compilers course :)
Next up, we’ll do the pair of contains functions:
bool BST::contains(const int x, BSTNode *t) const {
if(!t) return false; // base case
if(/* what goes here? */) return this->contains(x, /* what goes here? */);
if(/* what goes here? */) return this->contains(x, /* what goes here? */);
return true;
}
bool BST::contains(const int x) const {
return this->contains(x, this->root);
}
Problems with BSTs
What’s the one biggest problem we have in our code above?
Consider the tree created by running our insert function with the following input (in order):
1, 2, 3, 4, 5, 6, 7
- What is the shape of this tree?
How about this input (in order): 4, 2, 1, 3, 6, 5, 7
- What is the shape of this tree
In a naïve implementation, the tree can get so skewed due to insertion order that we end up with horrible runtimes ($O(n)$) again.
Options To Resolve
The key here is that we need to verify that our trees stay balanced throughout. The easiest way to handle this is to rebalance the tree as we insert to maintain some standard.
We’ll now discuss two commonly used methods, as well as go over some specialty trees that accomplish the same effect for different purposes.
AVL Trees
- An AVL (Adelson-Velsky and Landis) tree is a standard BST with an extra balance constraint
- In an AVL tree, the difference in height of the left and right subtrees of ANY node must be no greater than 1.
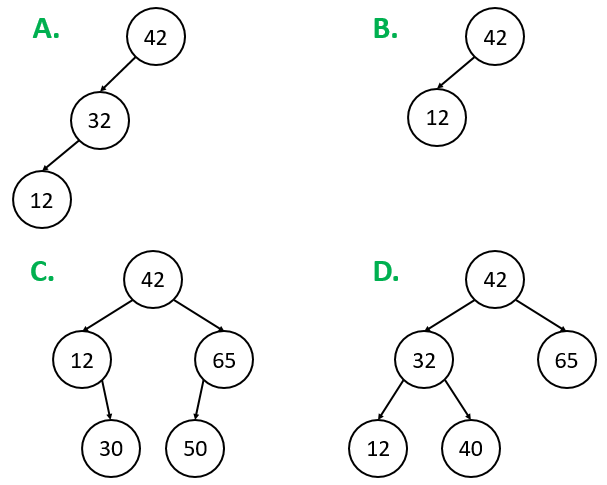 Which of these is not a valid AVL tree?
Which of these is not a valid AVL tree?
- To maintain this balanced property, we have to make modifications to insert and remove. Specifically, we need to re-order the tree when balance is violated.
- There are four main rotations we can perform on a node to rebalance it:
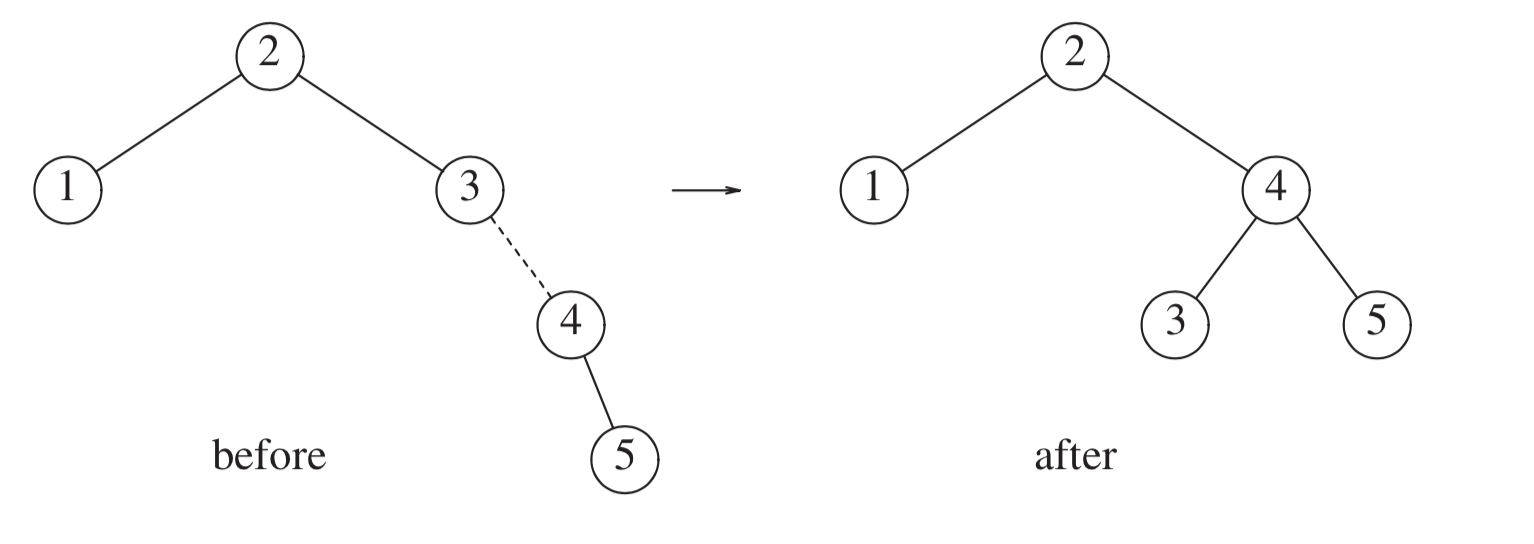
- Rotate left
- Used if the tree is right-heavy.
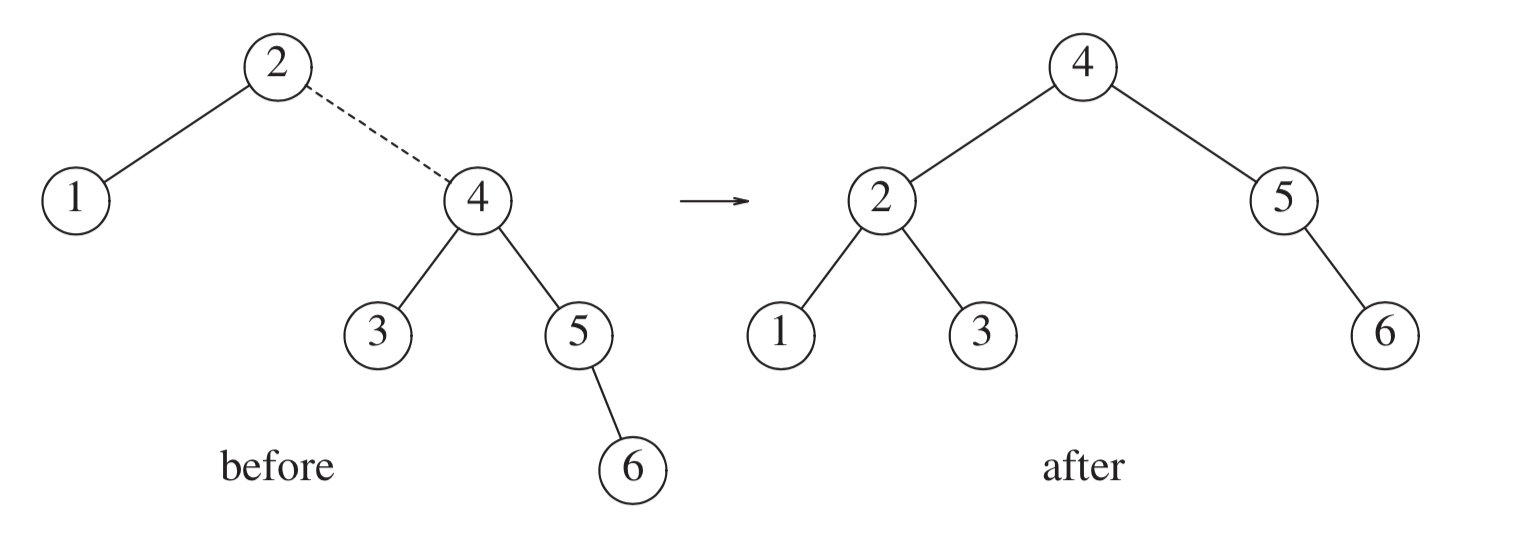
- Rotate right
- Used if the tree is left-heavy.
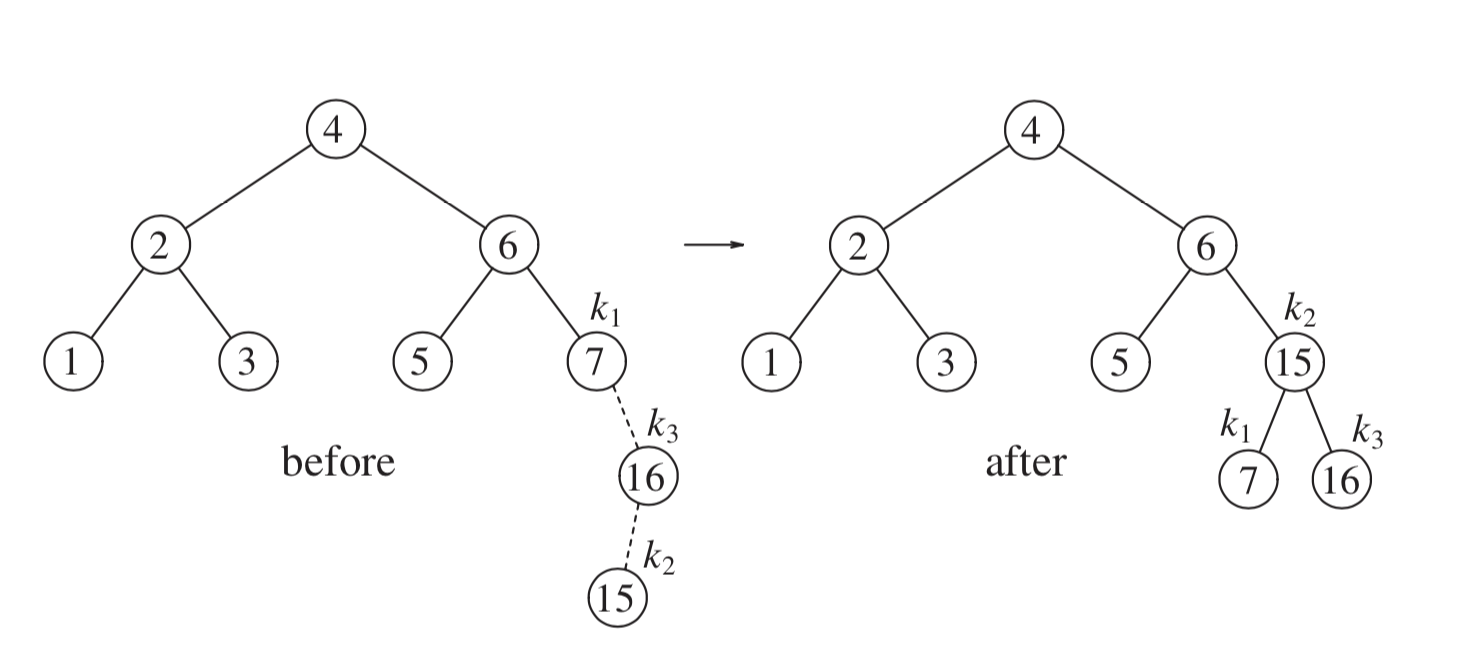
- Double left
- Used if the tree is right-heavy, but the right subtree is left-heavy
- Perform a right rotate on the left subtree, then a left rotate on the out of balance node.
- Double right
- used if the tree is left-heavy, but the right subtree is right-heavy.
- Perform a left rotate on the right subtree, then a right rotate on the out of balance node.
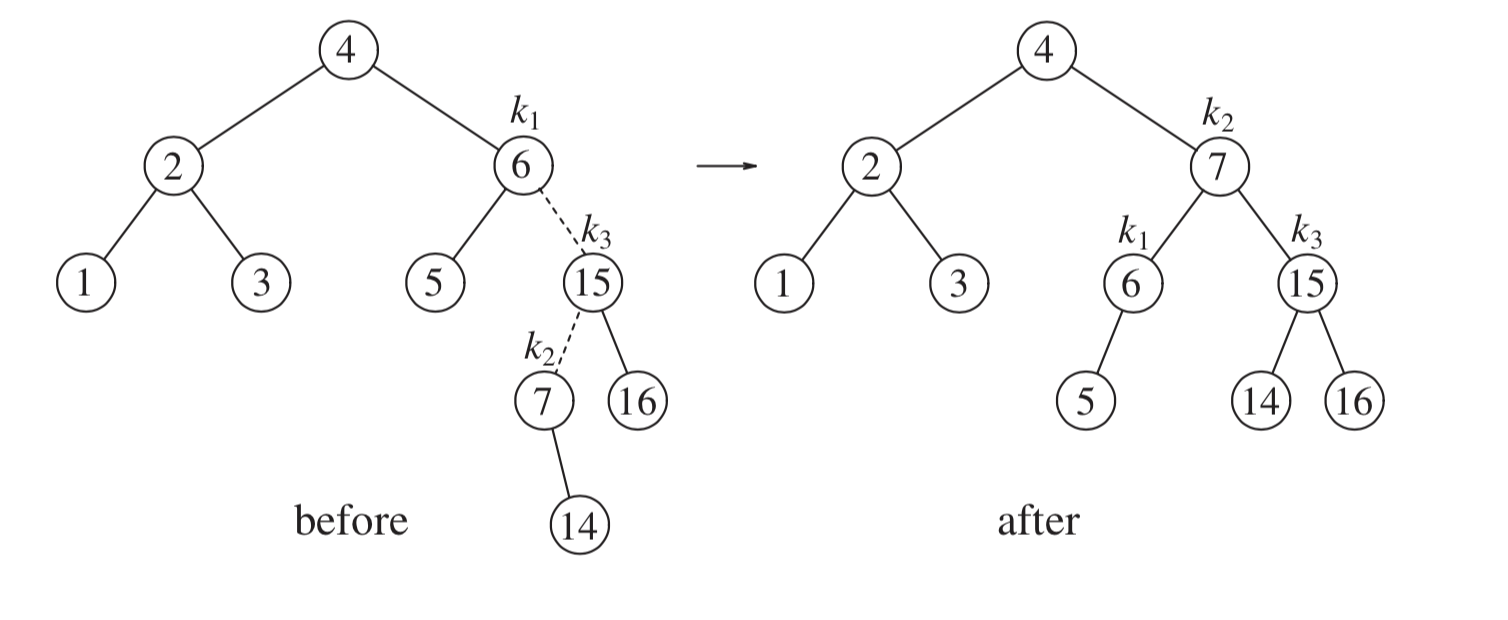
- Rotate left
- We perform these rotations as needed when inserting and removing nodes to guarantee that our tree will remain as balanced as possible, ensuring $O(\log (n))$ time for all three main operations.
Try doing AVL insertion for [1,7] in that order. What shape do you get?
- Downside of AVL: they’re not super fast for inserting and usually require another pass through to verify the balance constraint.
Red-Black Trees
- First conceptualized in 1972 by Bayer, but the modern implementation first appeared in 1978 by Guibas and Sedgewick.
- The tree trades strict balancing for speed, while still maintaining the logarithmic properties for all operations.
- A Red-Black tree is a BST for which the following properties must hold:
- All nodes are either “red” or “black” colored.
- The root must be “black”.
- If a node is “red”, it must not have any “red” children
- For any node u, every path from u to a null pointer must have the same number of “black” nodes.
Crucially, this means that being an AVL tree is a stricter property than being a Red-Black tree.
Is the following tree both a valid AVL and red-black, or just red-black?
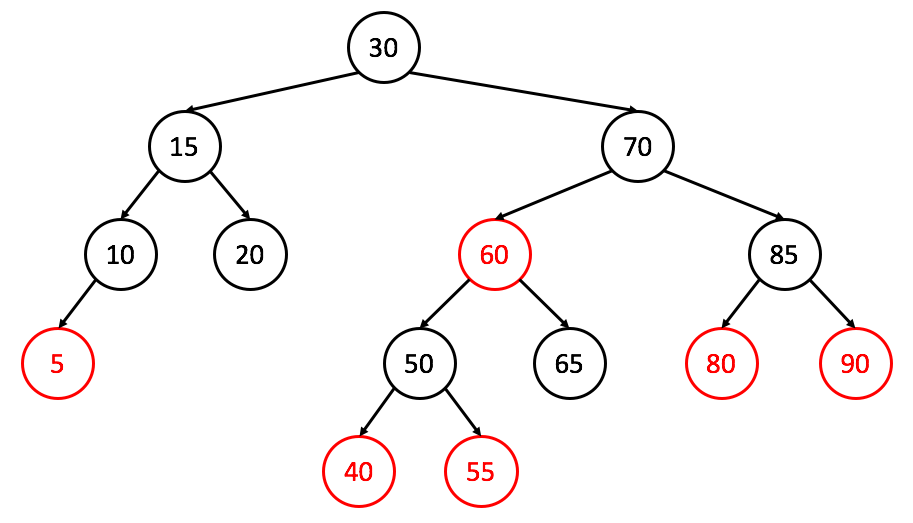
Is the following tree both a valid AVL and red-black, or just red-black?
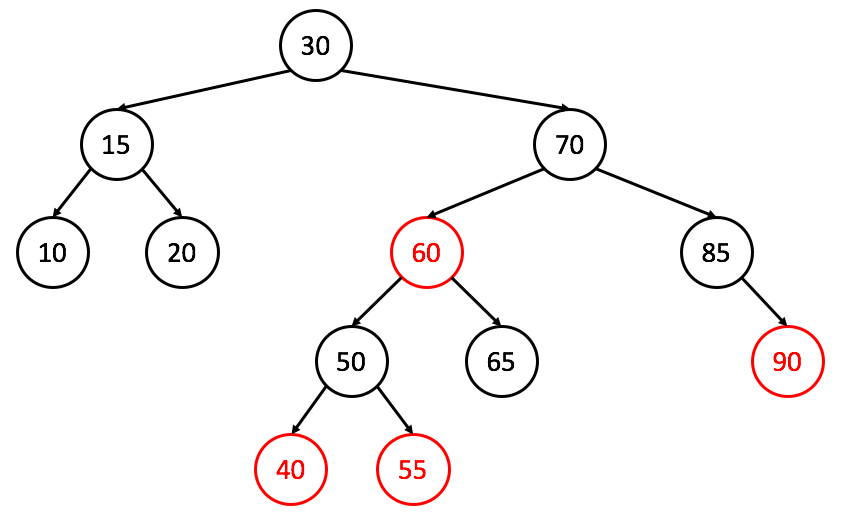
We won’t cover insertion or removal into a red-black tree (that’s for CSE 100!) but you can read about it here!
The book mentions a few more data structures; namely, B trees, B+ trees, and splay trees. We won’t cover those here, but feel free to check out chapters 4 and 12 of the book for B trees and splay tree implementations, and read the original splay tree paper here! Be warned, it’s a hefty paper.
That’s all folks! Good luck on midterm 2, and next time we’ll cover heaps and priority queues (with a special appearance from another BST type).